Graphing tangent, cotangent, cosecant, and secant functions

Unlike the sin and cosine functions, the other trigonometric functions can be thought of as rational functions. We can see how the other functions can be broken into the rational function form 

F(x) =      when placed in terms of sin and cosine. 

Starting with Tan and Cot…

    

Knowing that the zeroes of the numerator are x-intercepts and the zeroes of the denominator are horizontal asymptotes...

The x-intercepts of the tangent function will be the zeroes of the sine function and the zeroes of the cosine function will be horizontal asymptotic. The opposite can be seen when examining the cotangent function as a rational function. These locations can be seen on the graphs of the sine and cosine parent functions.

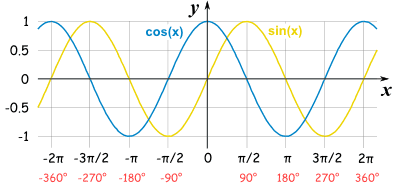
So, the horizontal asymptotes of the tangent and cotangent functions will correspond to the zeroes of denominator (cosine and sine respectively).

Because these zeroes occur for every half period of the regular sine/cosine graphs,
the periods of tangent and cotangent graphs will be π/B

                 f(x)=tan                                                                        f(x)=cot

The graphs of cosecant and secant can also be easily represented by rational functions when in terms of sine and cosine. The horizontal asymptotes of cosecant will correspond to the zeroes of sine. And the horizontal asymptotes of secant will correspond to the zeroes of cosine. 

Because the numerator is one when in rational form, the graphs of cosecant and secant will never cross the x-axis. Also, because value of cosine and sine is never greater than 1, the point that was the maximum/minimum of sin/cos function (the amplitude) now the opposite (either a minimum or maximum). 
The period for csc and sec functions will be 2π/B NOT π/B! This is because between two sets of asymptotes, the function will go to positive and negative infinity in the Y, not just one direction 
                                                                                         
                f(x)=csc         f(x)=sec



All the graphs will be translated the same way when the parent function is changed.
In the form f(x) = a (b (trig function(x)) -c) + d

Here are the functions with sliders to see how the different changes affect the graph.
Cotangent: https://www.desmos.com/calculator/dfbqrite7e
Tangent: https://www.desmos.com/calculator/pzxp6cwzd6
Cosecant: https://www.desmos.com/calculator/gzloezm4i8
Secant: https://www.desmos.com/calculator/duajze11qc