The Inverse Sine, Cosine, and Tangent Function

Jack Wischmeyer

Inverse Trigonometric Functions

Inverse Sine Function

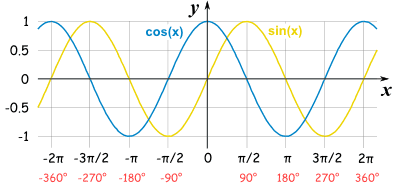
In order for an equation to be a function, we know that it must pass the Horizontal Line Test.  The three basic trigonometric functions that do not pass this test are the sine, cosine, and tangent functions.

As we can clearly see, this graph does not pass the horizontal line test within the range of the function.  However, in order to effectively use any of the three functions sine, cosine, and tangent, we must "change" the rules of the function.  By restricting the domain of the function to (-3.14/2,3.14/2), the function can possess the properties of holding it's whole range, and having the function pass the horizontal line test. 

Using the restricted domain function mentioned above, we can develop a new set of equations:

y=arcsinx                                                                                           

                                           Each of these functions are the inverse of it's counterpart.

y=arccosx                          

                                                

y=arctanx

Below is a useful table discussing the properties of the trigonometric functions:

         Function                                                     Domain                            Range                                   

y=arcsinx if and only if sin y=x                            (-1,1)                        (-3.14/2,3.14/2)

y=arccosx if and only if cos y=x                          (-1,1)                              (0,3.14)

y=arctanx if and only if tan y=x                   All Real Numbers            (-3.14/2,3.14/2)

As we learned earlier how the composite of a function and it's inverse equals x, the same properties are applied here.  If the domain of the trigonometric functions is (-1,1) and the range is (-3.14/2,3.14/2), then the following is true:

sin(arcsinx)=x     arcsin(sinx)=x

cos(arccosx)=x    arcos(cosx)=x

tan(arctanx)=x     arctan(tanx)=x

Ultimately, the basic properties of the trigonometric functions are not that different from what we have seen before.

Graphing tangent, cotangent, cosecant, and secant functions

Unlike the sin and cosine functions, the other trigonometric functions can be thought of as rational functions. We can see how the other functions can be broken into the rational function form 

F(x) =      when placed in terms of sin and cosine. 

Starting with Tan and Cot…

    

Knowing that the zeroes of the numerator are x-intercepts and the zeroes of the denominator are horizontal asymptotes...

The x-intercepts of the tangent function will be the zeroes of the sine function and the zeroes of the cosine function will be horizontal asymptotic. The opposite can be seen when examining the cotangent function as a rational function. These locations can be seen on the graphs of the sine and cosine parent functions.

So, the horizontal asymptotes of the tangent and cotangent functions will correspond to the zeroes of denominator (cosine and sine respectively).

Because these zeroes occur for every half period of the regular sine/cosine graphs,
the periods of tangent and cotangent graphs will be π/B

                 f(x)=tan                                                                        f(x)=cot

The graphs of cosecant and secant can also be easily represented by rational functions when in terms of sine and cosine. The horizontal asymptotes of cosecant will correspond to the zeroes of sine. And the horizontal asymptotes of secant will correspond to the zeroes of cosine. 

Because the numerator is one when in rational form, the graphs of cosecant and secant will never cross the x-axis. Also, because value of cosine and sine is never greater than 1, the point that was the maximum/minimum of sin/cos function (the amplitude) now the opposite (either a minimum or maximum). 
The period for csc and sec functions will be 2π/B NOT π/B! This is because between two sets of asymptotes, the function will go to positive and negative infinity in the Y, not just one direction 
                                                                                         
                f(x)=csc         f(x)=sec



All the graphs will be translated the same way when the parent function is changed.
In the form f(x) = a (b (trig function(x)) -c) + d

Here are the functions with sliders to see how the different changes affect the graph.
Cotangent: https://www.desmos.com/calculator/dfbqrite7e
Tangent: https://www.desmos.com/calculator/pzxp6cwzd6
Cosecant: https://www.desmos.com/calculator/gzloezm4i8
Secant: https://www.desmos.com/calculator/duajze11qc

Graphs of Sine and Cosine

When thinking of the graphs of sine and cosine, refer to the Unit Circle.

Graph of 


Characteristics of a Sine Graph:

• Sine is an odd function:  -f(x) = f(-x) 
• Symmetry about the origin - for every (x,y) there is a (-x,-y)
• y-intercept = (0,0) (unless shifted) - Due to the  on the Unit Circle

Graph of 


Characteristics of a Cosine Graph:

• Cosine is an even function:  f(-x) = f(x)
• Symmetry about the y-axis - for every (x,y) there is a (-x,y)
• y-intercept is (0,1) (unless shifted) - Due to the  on the Unit Circle

Period of Sine and Cosine Functions:
The periods of sine and cosine functions are found by 
Why?
Using the unit circle, one cycle is  radians, therefore the distance over one cycle of a sine or cosine function would be a fraction of the circle itself.

Variables affect on Sine and Cosine Equations:
Equation: 

What does each variable do to the parent graph of  ?
a: Amplitude of the equation - a vertical stretch or compress
b: Changes the Period of the function - horizontal stretch or compress
c: Phase shift - a shift left or right on the x-axis
d: Vertical shift - up or down on the y-axis

Trigonometric Identities 

In this chapter, multiple trigonometric identities are discussed. These include reciprocal identities, quotient identities, even/odd identities, co-function identities, and Pythagorean identities. 

Reciprocal Identities:

                   

                   

                       




Quotient Identities:

                    

Even & Odd Functions:
The definition of an even function is that a function is symmetric to the y-axis. For this to be true, the output must always be the same, regardless if the input has the same or opposite sign. Cosine and Secant are the only two functions that fits this definition.

                       
               

           

Co-Function Identities: (*Co-functions of complementary angles are always equal)

                                           

          

           

If you look at the triangle at the right, we can see that that sin(theta) equal to (a/c). Cos [(pi/2)-theta] is also equal to (a/c). Therefore, sin and cosine are referred to as co-function identities. 

Pythagorean Identities:
 

These identities are solely based on the right triangle and the Pythagorean Theorem, hence their name. 

Pythagorean Identity #1

This is how the first identity is derived:
The triangle at the right has a sin(theta) of a/c. Rearranged, (a=csintheta). cos(theta) of b/c. Rearranged, (b=costheta). The Pythagorean Theorem is a² + b² = c²
If we were to substitute sintheta for a and costheta for b, we get the following: 

At this point, we divide by c^2 and we get the first Pythagorean identity listed in the beginning. 

Pythagorean Identity #2

If we divide by cos²ө from the first formula, the cosines will divide out and you will have the inverse of cosine, leaving the second identity:

Pythagorean Identity #3

After dividing the formula above by tangent, we will be left with the inverse and secant over tangent, leaving us with the final Pythagorean identity: